B² Network技术实现：基于零知识证明验证承诺的比特币ZK-Rollup

原文作者： Stone , B² Network Research Lead

B² Network 是比特币上的一个 Layer 2 解决方案，主要利用将零知识证明验证承诺提交到比特币网络，允许挑战者发起欺诈证明进行挑战，以达到利用比特币网络的强大共识保证 B² Network 安全性的目的。

本文主要介绍以太坊上的 ZK-Rollup 和 OP-Rollup 的运行机制，介绍神奇的与非门电路，介绍承诺的作用，并利用这些机制和概念设计 B² Network 上的零知识证明验证承诺，进而说明零知识证明验证承诺如何在比特币网络执行以及如何保证 B² Network 的安全性。

以太坊上的 ZK-Rollup

ZK-Rollup 是一种区块链的二层扩展解决方案，通过聚合多个交易并利用零知识证明来确保这些交易批次的正确性和完整性，并在一层区块链网络上进行零知识证明的验证，从而利用一层网络保证二层网络的安全性。它旨在提高区块链系统的吞吐量，减少交易费用，同时保持高度的安全性和数据完整性。

ZK-Rollup 的运行过程大致如下：

1. 交易聚合和排序。用户向 ZK-Rollup 提交交易，交易将会被提交到 mempool 中。ZK-Rollup 的 Sequencer 从 mempool 中获取用户的交易并进行收集、排序，Sequencer 负责处理交易，更新账户状态，并最终生成一个代表这些更新的批次；

2. 状态转换和计算。所有的交易执行和状态更新都在链下进行。ZK-Rollup 的 VM（包括 zkEVM、zkVM 等不同的零知识证明智能合约执行引擎）计算新的账户状态，并处理如转账、智能合约交互等操作。同时生成必要的数据和证据来证明这些交易和状态更新是有效的，这里面包括新的账户状态和零知识证明；

3. 零知识证明生成。ZK-Rollup 的 Prover 利用零知识证明技术（如 zk-SNARKs 或 zk-STARKs）来创建一个证明，这个证明表明所有聚合的交易都是有效的，没有违反网络规则。这个证明不透露任何有关交易内容的信息，保护用户隐私，同时确保了数据的完整性和安全性。

4. 零知识证明验证。Aggregator 将批次的数据和零知识证明提交到一层区块链网络。这通常以一种压缩的形式发生，以减少所需的链上空间。一层区块链网络上的智能合约接收这些数据和证明，并验证证明的有效性。如果证明有效，合约将更新其记录的 ZK-Rollup 层的状态。

ZK-Rollup 的核心在于零知识证明的生成和验证。ZK-Rollup 的交易在链下执行，并在链下生成状态，通过 Prover 生成零知识证明，作为 ZK-Rollup 的承诺。这个承诺代表着 ZK-Rollup 上的交易正确、有效地执行，生成了正确的状态。一层区块链网络不需要验证 ZK-Rollup 的全部交易和状态，只需要验证承诺，承诺的验证是通过一层网络的智能合约进行零知识证明验证，即可确认 ZK-Rollup 的有效性。

因此，在以太坊的 ZK-Rollup 中，零知识证明数据是二层网络向一层网络提交的承诺。

以太坊上的 OP-Rollup

Optimistic Rollup (OP-Rollup) 是一种为了扩展区块链性能而设计的技术，它通过在链上保持最小的数据和执行尽可能多的计算在链下来实现。OP-Rollup 利用了“乐观”假设，即大部分交易都是诚实的，而不是立即验证每个交易的有效性，这样可以在一段时间后再进行验证，极大地提高了吞吐量和效率。

OP-Rollup 的运行过程大致如下：

1. 交易聚合和排序。用户向 OP-Rollup 提交交易，交易将会被提交到 mempool 中。OP-Rollup 的 Sequencer 从 mempool 中获取用户的交易并进行收集、排序，Sequencer 负责处理交易，更新账户状态，并最终生成一个代表这些更新的批次；

2. 交易的执行。OP-Rollup 的交易在链下执行，每个批次交易的执行，将导致旧的状态转变为新的状态，每个批次都会计算一个新的状态根（一种加密的“快照”表示整个系统状态），并将其提交到一层区块链网络；

3. 状态的验证。OP-Rollup 在提交交易批次时不立即进行复杂的验证，而是“乐观地”假设这些交易都是有效的，然后提交一层区块链网络。如果有观察者认为某个批次是无效的，他们可以提交一个欺诈证明来挑战该批次。在 Optimistic Rollup 解决方案中，欺诈证明是一种允许任何观察者挑战错误或恶意提交到链上的状态或交易的机制。Optimistic Rollup 利用欺诈证明来确保即使是“乐观地”接受的交易也可以在事后被证明是错误的，并相应地被撤销；

4. 挑战机制。挑战期是 OP-Rollup 提交状态确认后，有一个挑战窗口期，期间任何人都可以检查提交的批次，并在发现错误时提交欺诈证明，这通常是通过提交一个交易到一层区块链网络来实现，该交易声明了他们认为的错误并提供了相应的证据。 Arbitrum Rollup（一种 Optimistic Rollup 的解决方案）使用一种称为“交互式验证游戏”的过程来解决挑战。在这个过程中，挑战者和提交者之间进行一系列的回合，逐步缩小他们对哪里出错的意见不一致的范围（采用的是二分查找法快速定位错误的交易位置）。最终，这个过程将确定错误发生的确切位置。一旦错误被确认，原始的批次将被撤销，并对提出错误的验证者进行处罚。如果挑战失败，则挑战者可能会失去他们为发起挑战而抵押的资金；如果挑战成功，则挑战者可以获得成功发起挑战赢得的奖励资金。

OP-Rollup 的核心在于欺诈证明和挑战机制。OP-Rollup 首先会“乐观”地认为所有交易都正确执行，然后在一层网络将计算编译为合约内虚拟机（AVM、OVM）的字节码，发布字节码的承诺。OP-Rollup 的承诺验证，需要进行交易计算，并获得字节码，然后验证承诺。一旦有观察者发现有承诺不匹配的批次，观察者将会通过挑战机制生成欺诈证明，获得奖励。

以太坊的 OP-Rollup 首先“乐观”地确认和提交承诺，然后利用挑战机制，允许任何人对提交的承诺进行挑战，最终通过承诺和挑战确保 OP-Rollup 得到验证和确认。

神奇的与非门

与非门（NAND gate）是数字逻辑中的一种基本逻辑门，它实现了逻辑与（AND）操作后的逻辑非（NOT）操作。与非门的特性使其成为能够构造任何其他逻辑门和复杂逻辑电路的基础。以下是如何使用与非门构造逻辑门（如与门、或门、异或门）以及加法门和减法门的详细介绍：

1. 与非门基础

与非门有两个输入，当且仅当两个输入都为 1 时，输出为 0 ；在所有其他情况下，输出为 1 。这可以用逻辑表达式表示为 A NAND B。

2. 构造基本逻辑门

与门（AND）

要使用与非门构造与门：

• 第一步：将两个输入连接到一个与非门。

• 第二步：将该与非门的输出连接到另一个与非门的两个输入端。

• 结果：第二个与非门的输出就是与门的结果。

或门（OR）

要使用与非门构造或门：

• 第一步：将每个输入分别通过一个与非门（自己与自己），产生两个非门的效果。

• 第二步：将这两个与非门的输出作为一个与非门的输入。

• 结果：该与非门的输出就是或门的结果。

异或门（XOR）

要使用与非门构造异或门（更复杂一些）：

• 第一步：构造两个与非门，每个输入都连接到其中一个。

• 第二步：将第一步中的两个与非门的输出作为第三个与非门的输入。

• 第三步：将原始输入 A 和第一个与非门的输出连接到第四个与非门，将原始输入 B 和第二个与非门的输出连接到第五个与非门。

• 第四步：最后，将第四个和第五个与非门的输出连接到第六个与非门。

• 结果：第六个与非门的输出就是异或门的结果。

3. 构造加法门

半加器（Half Adder）

半加器是一个简单的加法器，它可以处理两个位的加法，并产生和（sum）和进位（carry）。

• 和：使用一个异或门来生成和。

• 进位：使用一个与门来生成进位。

• 使用与非门构造这些基本门，然后将它们组合起来形成半加器。

全加器（Full Adder）

全加器考虑了来自低位的进位输入。

• 第一步：构造两个半加器，第一个处理 A 和 B，第二个处理第一个半加器的和与进位输入 C。

• 和：第二个半加器的和输出。

• 进位：两个半加器的进位输出通过一个或门连接。

• 使用与非门构造半加器和或门，然后组合它们形成全加器。

4. 构造减法门

半减器（Half Subtractor）

半减器处理两个位的减法。

• 差：使用一个异或门生成差。

• 借位：使用一个与非门和非门来生成借位。

• 使用与非门构造异或门和其他所需逻辑，然后组合它们形成半减器。

全减器（Full Subtractor）

全减器考虑了来自高位的借位。

• 第一步：构造两个半减器，第一个处理 A 和 B，第二个处理第一个半减器的差与借位输入。

• 差：第二个半减器的差输出。

• 借位：两个半减器的借位输出通过一个或门连接。

• 使用与非门构造半减器和或门，然后组合它们形成全减器。

5. 构造乘法门

二进制乘法

实现两个二进制数的乘法。

• 第一步：使用与门进行位乘法。

• 第二步：使用全加器串联进行连续的加法。

• 第三部：实现移位和累加。

6. 构造寄存器

D 触发器

存储一位二进制信息。

• 第一步：使用与非门创建锁存器（Latch）。

• 第二步：将锁存器扩展成触发器（ Flip -flop）。

寄存器

存储多位二进制数。

• 将多个 D 触发器并行连接，每个存储一位。

7. 构造时钟

振荡器

提供周期性的时钟信号。

• 使用与非门创建反馈回路，产生连续的振荡。

结论

与非门因其能够构造任何其他逻辑门和复杂电路的能力而被称为“通用逻辑门”。通过上述方法，可以利用与非门构建出复杂的加法、减法、乘法以及存储和时钟电路，这是计算机和数字系统中进行算术运算的基础。在现代集成电路设计中，与非门因其简单性和多功能性而广泛使用。

在 B² Network 的实践中，通过与非门可以构造任何的计算逻辑。

密码学中的承诺

承诺在密码学和区块链中应用非常广泛，像 SHA 256、Merkle Tree、零知识证明中的 KZG 都是承诺，像上文中介绍的 ZK-Rollup 将零知识证明作为 Rollup 的承诺，OP-Rollup 将虚拟机内的字节码作为 Rollup 的承诺。

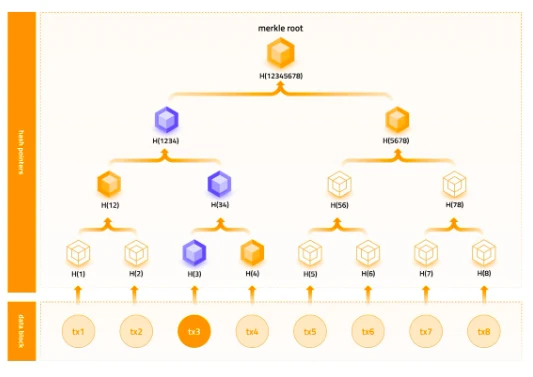
我们通过 Merkle Tree 来详细说明如何使用承诺：

1. commit：Prover 将所有的 value 计算哈希，哈希作为二叉树的叶子节点，不断向上进行哈希计算，最终生成 Merkle Tree，发布 tree root hash 作为承诺。

2. reveal：Prover 揭露一个叶子节点对应的 value，以及其 branch。

3. check：Verifier 通过揭露的 value、branch 计算哈希，最终与发布的承诺进行对比，进行验证。

如下图示例：

1. commit：Prover 将 tx 1、tx 2 ……tx 8 分别计算哈希，获得 H( 1)、H( 2)......H( 8)，不断两两进行哈希计算，最终生成图中的二叉树结构，即 Merkle Tree，将 Merkle Tree 的 root 节点的值 H( 12345678)作为承诺进行发布。

2. reveal：Prover 揭露一个叶子结点对应的 value，如 tx 3 ，以及其 branch（H( 4) -> H( 12) -> H( 5678)）。

3. check：Verifier 通过揭露的 tx 3 和 branch（H( 4) -> H( 12) -> H( 5678)）进行计算并验证承诺：

• 计算 tx 3 的哈希 H( 3)

• 将 H( 3)与 branch 中的 H( 4)进行哈希，得到 H( 34)

• 将 H( 34)与 branch 中的 H( 12)计算哈希，得到 H( 1234)

• 将 H( 1234)与 branch 中的 H( 5678)计算哈希，得到 H( 12345678)

• 将 H( 12345678)与公布的承诺进行验证

B² Network 的零 知识证明验证承诺

B² Network 是构建在比特币网络的 ZK-Rollup 二层解决方案。

Bitcoin 上 ZK-Rollup 的限制

由于比特币的图灵不完备限制，导致比特币网络上没有办法进行零知识证明的验证，因此 ZK-Rollup 的传统解决方案，在一层区块链网络验证零知识证明的实现方式，是没办法在比特币网络上实现的。

ZK-Rollup 只将零知识证明和 Rollup 的数据聚合通过 Taproot 写入比特币网络，只能保证 ZK-Rollup 的数据锚定在了比特币网络，无法被篡改，但是无法保证 ZK-Rollup 的交易的有效性、正确性，也没办法利用比特币网络的强大共识能力保证二层 ZK-Rollup 的安全性。

因此，一定需要在比特币网络上进行 ZK-Rollup 的确认。

零知识证明与算术电路

零知识证明

在零知识证明中，算术电路用于构建一个证明，证明者知道某些秘密信息，而不需要透露这些信息本身。

零知识证明使用算术电路生成证明：

• 生成证明

  一旦算术电路建立，证明者将使用他们的秘密输入来计算电路的输出。在这个过程中，证明者还会生成额外的信息（如零知识证明特有的承诺和随机数），这些信息用于构建证明。

• 验证证明

  证明者将他们的证明发送给验证者。验证者不知道证明者的秘密输入，但他们有电路的描述和证明者的证明。验证者通过执行电路的相同计算，并比较其结果与证明者提供的证明，来验证证明的有效性。

算术电路

算术电路通常表示为一个有向无环图（DAG），其中每个节点代表一个算术操作，边代表操作之间的数据流。输入节点代表电路的输入值，通常是一些数字或变量，而内部节点代表算术操作。电路的输出是最终的计算结果。

算术电路中的基础电路门：

• 加法门（ Addition Gate）

• 乘法门（Multiplication Gate）

根据上文中与非门的介绍，算术电路是可以通过将加法门转换为与非门，将乘法门转换为与非门，最终算术电路转换为基于与非门的逻辑门电路。

零知识证明验证承诺

零知识证明的验证程序本身是一个算术电路，通过将算术电路转化为基于与非门的逻辑门，实际上可以将零知识证明的验证程序转化为基于与非门的逻辑门电路。

与非门通过比特币脚本实现，将 Bit Value Commitment 作为输入和输出组装成逻辑门，实现逻辑门约束。

可简记为 <hash_c 0> <hash_c 1> <hash_b 0> <hash_b 1> <hash_a 0> <hash_a 1> OP_GATECOMMITMENT ，对应的 unlocking script 是 <preimage_a> <preimage_b> <preimage_c> 。

实际上，可以通过比特币脚本实现与非门，再由与非门构造出加法门和乘法门，加法门和乘法门组合成算术电路，最终构造出零知识证明的验证程序。但是由于涉及的门电路非常多，构造出的比特币脚本也非常庞大，无法在比特币网络上真正运行。

将 Bit Value Commitment 作为输入和输出组装成逻辑门，每一个带有不同输入和输出的逻辑门作为叶子节点，组合成电路二叉树，发布的 Circuit Taproot 是二叉树的 root，减小了发布的尺寸。

Circuit Taproot 作为 B² Rollup 在一层区块链网络比特币上提交的承诺。不同于传统的 ZK-Rollup 可以在一层网络执行验证，B² Rollup 无法在比特币上直接执行验证。但是可以参考 Optimistic Rollup 的方式，针对承诺提供挑战机制，通过挑战机制完成 Circuit Taproot 承诺的确认。

验证和响应协议

不同于 BitVM 需要提前签署两方间的链下交易。B² Network 采用发布锁定奖励的 UTXO 交易，解锁脚本是一个 Taproot 脚本。

具体的解锁 Taproot 脚本是 Prover 提前将 Circuit Taproot Tree 的每个 branch 生成脚本，并给定输入的哈希。Challenger 利用 preimage 执行脚本，如果执行的 output 和 Prover 的提交不一致，就能利用 MAST （Taproot Merklized Abstract Syntax Tree，默克尔抽象语法树）解锁整个 Taproot，从而获得锁定的奖金。

由于零知识验证程序的运行成本很小，也非常快速，因此比特币网络上的用户都可以充当 Challenge 机制的观察者，验证 B² Rollup 提交的承诺，一旦发现承诺不一致，可以立即发起挑战。

挑战机制类似于 Arbitrum Rollup 的“交互式验证游戏”，不断寻找错误执行的逻辑门计算。为了在众多逻辑门中找到错误的一个，将会使用二分查找的方式，执行门电路比特币脚本。最快找到错误分支的挑战者，可以在比特币网络上解锁锁定奖励的 UTXO，从而获得奖励。

同时，Taproot 锁定脚本中的一个分支是时间锁脚本，当没有 Challenge 成功挑战，Prover 将在挑战期结束后，通过时间锁脚本解锁 UTXO，取回奖励。

总结

B² Network 通过 Ordinals Protocol，将 rollup 的 data 和 proof 聚合后写入 Tapscript 中，利用不同的去中心化存储协议保存 rollup 明细数据，有效地保证了 rollup 的 data availability。

B² Network 通过将 zero-knowledge proof verification commitment 记录在 Bitcoin 上，允许任意的观察者针对 commitment 进行挑战的机制，可以继承 Bitcoin 的安全性，在 Bitcoin 上共识 rollup 的数据。