比暴力破解更聪明，研究者提出针对比特币弱私钥的点阵攻击方式

私钥对密码货币的重要性不言而喻，在这个世界，无时无刻都有人在打着破解比特币私钥的主意。

其中最粗暴的方式，就是通过穷举的方式暴力碰撞比特币私钥，LargeBitcoinCollider(LBC)就是这样的一个组织，其使用了明显线性的暴力搜索算法，而这样的方法，在量子计算学没有得到实质性进展前可以说是比较愚蠢的。

而对于已泄露的公钥而言，使用平方根离散对数算法，则是恢复这类短私钥的更为有效的方法，而来自宾夕法尼亚大学的博士后研究员Joachim Breitner和来自加利福尼亚大学计算机科学与工程学院的副教授Nadia Heninger，则联合进行了一项称为《 针对密码货币弱ECDSA签名的点阵攻击 》的研究。

在这项研究中，我们看到比特币、以太坊和瑞波区块链，以及HTTPS和SSH中的私钥，会有数种不安全的使用方式，因而它们可能会被破解。由此产生的数字并不大，在实验中，研究者共计算出了300多个比特币私钥（余额约为0.00818975 BTC），以及30.40 XRP，但实验却告诉我们，想要正确使用密码货币，其实是一件非常棘手的事情，如果你做得不对，那么你很可能会丢失资金。

当你使用ECDSA（椭圆曲线数字签名算法）创建密码学签名时，你需要提出一个256位随机数的nonce。每一次签名时，使用不同的nonce是非常重要的，否则其他人很容易能拿到你的签名，并使用相对简单的数学计算你的私钥，而有了你的私钥，他们就可以花掉你所有的比特币。实际上，有证据表明： 一直有人在监视区块链上是否存在这种重复的nonce，如果检测到，他们就会计算出相应私钥，并从中提取资金 。

这种攻击方式知道的人并不多，但对于密码学社区而言，这并不是什么新的东西，攻击者可以根据使用不同，但相似的nonce计算私钥：例如，如果它们彼此靠近（只有低位不同），或者它们的差别正好是2的大幂（只有高位不同）。这使用了一种基于点阵（lattices）的强大技术。这篇论文的主要贡献，在于连接了密码学和密码货币，看看这些漏洞是否真实存在。

事实上，密码货币当中的确存在这样的漏洞，好在数量并不是很多，但它们确实存在着，而且显示是有多个来源。不幸的是，我们很难找出是谁做了这些签名，以及用了什么代码，所以我们只能猜测这些错误的原因。大量受影响的签名与多重签名交易有关，因此，我们认为，硬件token可能是导致这种情况的原因。

尽管我们无法确定导致这些问题的具体实现，但我们仍然可以观察到一些关于它们的有趣细节。最让人好奇的，当然是这个：

其中一组签名是由一个攻击者创建的，其清空了泄露密钥的账户（例如那些使用弱密码创建的，或以其他方式泄露到互联网上的私钥）。

因此，看起来很像攻击者建立了一个监控区块链的程序，其会清空已泄露的账户。

(图片来自： pexels.com )

我们需要担心吗？

大概不需要。官方的区块链客户端在这方面做得很好（至少在这一部分），它们使用了正确的随机nonce，所以作为一个用户，你没有太过担心 。事实上，自2016年以来，比特币客户端使用了确定性签名（ RFC6979 ）方案，这完全消除了过程中的随机性需求。

如果你使用的是非标准库，或者你自己编写了密码例程（只有当你有非常好的理由时，才应该那么做），那么你应该确保它们使用了RFC6979（关于这一话题，比太钱包团队在2014年就发过一篇文章《 分分钟搞懂 RFC6979 》）。这在嵌入式设备或或硬件token上更为重要，因为很难找到随机性的好来源。

以下是论文的部分译文：

标题：针对密码货币弱ECDSA签名的点阵攻击（Lattice Attacks）

作者：Joachim Breitner 和 Nadia Heninger

所在机构 ：DFINITY Foundation, Zug, [email protected] 加州大学（UC）, San Diego, [email protected]

摘要。在这篇论文中，我们对包含在公链和互联网扫描的数字签名进行密码分析攻击，由此计算出了数百个比特币私钥，以及数十个以太坊、瑞波币、SSH以及HTTPS私钥。ECDSA签名算法要求生成每个消息的秘密nonce。这个nonce必须完全一致地生成，否则攻击者可利用nonce偏差计算长期签名密钥。我们使用一种基于点阵（lattice-based）的算法来解决隐藏数问题，以有效地计算由于多个明显的实现漏洞，而与有偏差的签名nonce一起使用的私有ECDSA密钥。

关键词：隐藏数问题，ECDSA（椭圆曲线算法）、点阵（Lattices）、比特币、密码货币

一、简介

ECDSA签名算法的安全性关键，依赖于正确生成用作临时私钥的每个签名nonce值。众所周知，如果使用ECDSA私钥签署两个具有相同签名nonce的消息，则长期的私钥就很容易去计算。[18,7,37,13,11,8]

然而，重复的nonce值并不是唯一可使ECDSA密钥不安全的偏差类型。实际上，ECDSA签名nonce中的任何不一致性，如果有足够多签名的话，都可以让私钥暴露。在这篇论文中，我们对从比特币、以太坊和Ripple区块链以及ssh和https收集的ECDSA签名进行了基于点阵的密码分析攻击，并有效地计算了数百个比特币私钥和少量以太坊和SSH私钥。

此外，我们还发现了大量的比特币、以太坊、Ripple、ssh和https私钥因为重复的签名而泄露了。我们应用的点阵攻击，是基于隐数问题的求解算法。虽然隐藏数问题，在很多密码学文献当中，是基于侧通道攻击[5,14]用于恢复私钥的一种流行工具，但据我们所知，我们是第一个观察到这种技术可适用于密码货币的签名。通过这种技术，我们计算了大约300个比特币私钥，共计0.00818975 BTC，以及30.40 XRP，这些资金仍然留在原账户当中。

对于椭圆曲线离散对数问题，我们使用的攻击方式，显然要比幼稚的暴力攻击或最先进的算法要快得多。使用像Pollard rho [28]这样的平方根时间算法是可行的，这样我们可对小部分我们发现的64位或128位nonce目标进行有针对性的攻击； 而对比特币区块链中大约2^30个签名进行攻击，将需要比我们所获得的多得多的计算资源 。相比之下，对于所有区块链，我们的计算总共花费了40年的CPU时间（注：CPU时间即反映CPU全速工作时完成该进程所花费的时间），这些计算是用Python实现的。

nonce漏洞分为几个类，而这次研究表明我们发现了几个独立的实现漏洞。当所使用的nonce要比我们预期要短时，我们首先使用隐数问题算法来发现长期ECDSA签名密钥，并用长度为 64位、110位、128位以及160位的nonce找到密钥。

道德准则：我们无法验证这些漏洞的存在，除非实际计算易受攻击地址的私钥。对于密码货币，这些密钥可使我们或任何其他攻击者能够盗走关联账户中的资金。对于ssh或https，这些密钥将使我们或任何其他攻击者能够模拟终端主机。我们没有这样做，在我们的研究过程中，我们没有转移走任何密码货币，或主动攻击我们自己。我们的研究完全是被动的，只需要观察交易或通用网络测量。然而，鉴于我们发现一些证据， 表明其他攻击者已通过已知漏洞（包括重复的nonce以及把私钥在线发布）而清空了相关泄露的密码货币用户账户 。我们预计，一旦这个缺陷被恶意者利用，相关用户就会受到影响。

我们试图向少数我们能识别的团队披露这些缺陷，但在大多数情况下，我们无法向特定的供应商、维护人员或用户披露相关漏洞。

对策。我们在本论文中所讨论的所有攻击，都可以通过使用确定性的ECDSA nonce 生成 [29]工具来防止，这已经在默认的比特币和以太坊库中实现了。

二、相关的工作

隐藏数问题和ECDSA 。隐藏数问题，以及我们用来解决它的基于点阵的算法，是由Boneh和Venkatesan提出的，他们用它来证明计算Diffie-Hellman [6]最重要位的困难。

Howgrave Graham、Smart[19]、Nguyen以及Shparlinski [26]应用了隐藏数问题，来显示如果攻击者可以学习一些当前最重要的签名nonce位，则DSA和ECDSA签名方案是不安全的。从那时起，这种技术在实践中被应用于侧通道攻击[5,14]。

重复的DSA/ECDSA签名 。很多研究工作已检查到DSA和ECDSA当中由于重复签名nonce而存在的漏洞。Heninger、Durumeric、Wustrow和Halderman[18]在2012年通过从SSH handshakes搜索重复的DSA签名nonce，使得1%的SSH主机密钥被暴露。他们把问题主要追溯到低资源设备上随机数生成的实现漏洞。

Bos, Halderman, Heninger, Moore, Naehrig和 Wustrow [7] 在2013年记录了比特币区块链中重复出现的nonce，以此作为关于椭圆曲线密码技术应用更广泛研究的一部分。Valsorda在2014年研究了重复的比特币nonce[37]。Courtois, Emirdag以及 Valsorda[13] 在2014年研究了重复的比特币nonce，并指出其有可能对密钥产生威胁。Castellucci 和 Valsorda在2016年研究了重复nonce以及弱密钥变体，以及比特币密钥当中存在的重复nonce [11]。Brengel和Rosow在2018年研究了来自同一密钥签名中的重复nonce，并在比特币区块链中不同密钥签名之间链接了泄露的nonce [8].

密码货币中的密钥生成问题 。在2013年，安卓SecureRandom的一个主要漏洞，被指责是导致很多比特币安卓钱包用户被盗的原因，这是由错误的随机数生成器生成了重复的ECDSA签名nonce [20,22]所致。2015年，Blockchain.info的安卓应用，被发现生成了重复的私钥，因为该应用的种子是从random.org导出的，而该网站当时出现了403问题，并重定向到他们几个月前的https URL [35]。

针对密码货币的密码分析 。大型比特币对撞机（The Large Bitcoin Collider）是一个针对比特币私钥的暴力搜索项目，其使用了明显线性的暴力搜索算法 [30]，并最多搜索到54位的密钥。对于已泄露的公钥而言，使用平方根离散对数算法 [28,34]是恢复这类短私钥的更为有效的方法，但目前我们还没有看到有人在做这方面的尝试。

三、椭圆曲线数字签名算法（ECDSA）

椭圆曲线数字签名的公共域参数包括有限域上的椭圆曲线E，和E上n阶的基点G。私有签名密钥是整数d modulo n，而公共签名验证密钥是点Q = dG。椭圆曲线公钥可通过提供公共点Q的x和y坐标来表示未压缩形式，也可以通过仅提供x坐标和y值的单个奇偶校验位来表示为压缩形式。[9]

要对消息哈希h进行签名，签名者选择每个消息的随机整数k modulo n，计算

3.1密码货币中的ECDSA

比特币 [23],以太坊 [10]和瑞波 [33] 都是使用的椭圆曲线secp256k1 [9]。

比特币地址是通过使用sha-256和RIPEMD-160算法反复哈希未压缩或压缩的ECDSA公钥，从而生成地址的。

而以太坊地址是未压缩ECDSA公钥的Keccak-256哈希的最后20个字节，其中Keccak-256算法是SHA-3算法的一个早期版本。以太坊公钥并不明确地随签名一起提供，相反，签名包含一个额外的字节 v，其允许从签名中派生公钥。

瑞波地址是通过SHA-256和RIPEMD-160算法反复哈希压缩公钥而来的，并连接哈希的各个部分。

为了论文分析目的，在以上这些密码货币当中，只有在地址签名一笔交易之后，才会显示出ECDSA公钥。

通过签名，比特币和瑞波会明确显示未压缩或压缩格式的ECDSA公钥；而在以太坊中，客户端必须使用密钥恢复从签名本身派生出公钥。

ECDSA签名用于对一笔交易的发送方进行身份验证。地址可以是单个签名的，其对应于单个公钥，也可以是多签名地址，这些地址需要n个公钥集当中至少k个公钥的有效签名，这样才能完成一笔交易。通常用户在进行每一笔交易时，应使用新的地址[2]。

签名规范化。ECDSA签名具有签名(r, s)和 (r, −s) 的属性，其将用相同的公钥进行验证。2015年10月份，比特币在签名过程中引入了一种变化，即在签名中使用s和−s mod n的较小值，以使签名具有唯一性。以太坊和瑞波也进行了这种类型的签名规范化，这会影响到我们的攻击。

3.3 针对ECDSA的基本攻击

如果攻击者知道了用于生成一个ECDSA签名的每条消息（per-message）的nonce k，则长期密钥d是易于计算的，因为

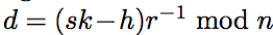
众所周知，如果使用相同的密钥，将相同的nonce k签署两则不同的消息h1和h2，那么这个密钥就会泄露。 设(r1, s1)为消息哈希h1上生成的签名，（r2，s2）为消息哈希h2上的签名。我们马上得到r1 = r2，因为r1 = r2 = x(kG)。然后我们就可以计算，并恢复如上所述的密钥。

四、针对ECDSA的点阵攻击

在随机modulo n上，签名nonce k 也必须完全一致地生成，否则，可使用解决隐数问题的技术，来求解密钥d 。

关于具体攻击解释，请看 原论文 。

后记：对于密码货币持有者而言，最为重要的，就是掌握安全的保管方式以及私钥生成方式，选择好的钱包会是非常重要的，官方钱包虽然“笨重”，但相对来说是更安全的。